2. Introduction to Vectorization

What is Jax? Jax is a Python library for high-performance numerical computing and array operations capable of automatically run on different hardware (e.g. it can run on Graphical Processing Units—or GPUs—which are commonly used for training ML models). The main part of Jax you’ll be interacting with (for now) comes from:

import jax.numpy as jnp

This portion of Jax introduces its main building block: multi-dimensional arrays. Unlike other similar libraries that offer similar array-based framework (e.g. NumPy), Jax has some features that will make it possible for us to efficiently build and train ML models. Specifically, it will allow us to easily and accurately (no approximations!) compute gradients of functions written in Jax calls, which will become useful for training models (though more on that at a much later part of the course).

Array operations: the building blocks behind ML code. You may be wondering, why do we need arrays for ML? This is because, as you will see throughout this course, all of the code we will write can be conveniently expressed in terms of array operations. Jax will make these fast for us so we can spend more time thinking and less time waiting for your code to run. It’s therefore important that we re-learn how to think and how to write algorithms in terms of array operations.

Vectorization: a paradigm shift. Vanilla Python code is slow, and for many practical purposes, that’s not a problem. For training ML models, however, it does become a problem. Unlike in previous classes you may have taken, where you were encouraged to write loops, if/else-expressions, and more, in Jax we’ll take a different paradigm: we will avoid writing loops and if/else-expressions. By this, we don’t mean that you completely let go of all your previous coding knowledge. It will come in handy when reading in data, creating visualizations, etc. But for the compute-heavy part of your code, we will rely on Jax library calls to do the work for us. This practice—of avoiding writing loops and if/else-expressions in the compute-heavy part of the code—is known as vectorization. Vectorization in Jax is implemented to be very, very fast under the hood.

Idea: The idea behind vectorization is to expend more memory than typically needed in order to rely on the Jax internals to do its magic. For example, suppose we wanted to compute the sum of squares:

\[\begin{align*} 0^2 + 1^2 + 2^2 + 3^2 + 4^2 + \dots + (N - 1)^2 = \sum\limits_{n=0}^{N-1} n^2. \end{align*}\]

The typical, loop-based way to implement this would be:

total = 0.0
for n in range(N):
    total += n ** 2.0

In contrast, in the vectorized paradigm, we will create an array, \([0, 1, 2, \dots, N-1]\), using up space to store \(N\) elements, instead of just total. Then, we’ll use Jax operations to square and sum the elements of the array:

total = jnp.sum(jnp.arange(N) ** 2.0)

This is much faster than our original loop-based implementation. We’ll introduce all of the Jax library calls below so you can begin writing vectorized code.

Outline:

1. We’ll introduce the basics of Jax

2. Once you have the basics down, we will show you how to vectorize code you would normally have written using loops

Acknowledgement. Parts of this tutorial have been adapted from this NumPy tutorial.

2.1. Tips and Advice

Reading Documentation. Jax was built to imitate another popular library, NumPy. Just about all functions implemented in NumPy have a corresponding Jax version with the same interface. Often, you’ll find the internet has more resources on NumPy than on Jax (since Jax is newer) – that’s ok! The same tips often translate. Moreover, you may consider purposely looking up NumPy documentation to answer your questions because they often have examples (which the Jax documentation usually does not have).

• You can find jax.numpy documentation here.

• You can find numpy documentation here.

Caution: do NOT mix up NumPy arrays with Jax arrays. You can technically call Jax functions on NumPy arrays and vice versa. PLEASE DO NOT DO THAT. Doing so will not throw any errors, but may result in other bugs that are difficult to find. One way you can keep yourself from making this mistake is: do not import NumPy at all.

Unlike NumPy arrays, Jax are immutable. By this, we mean that once created, they cannot be altered. Any operation you perform on a Jax array will return a brand new array. For example, in Numpy you can set the 0th index of an array equal to some value with arr[0] = value, but in Jax, this will throw an error. You might think: this seems really inefficient—does this mean we are constantly burdening our computer by requesting for memory? Jax actually leverages this property to speed things up (this is not something we’ll cover in the class). We note this property here because it’s important to be aware of it! Any operation you perform on a Jax array needs to be saved into a new variable.

When unsure, play! Whenever you find yourself unsure of how something works, or confused by all the jargon in the documentation, that’s totally normal. To gain intuition, we recommend you tinker and play: try out little bits of code on small arrays in a controlled setting and see what happens.

2.2. Properties of Arrays

So what does an array look like? Here’s an example:

a = jnp.array([[1.0, 4.0, 8.0], [0.1, -1.0, -5.0]])
print(a)

[[ 1.   4.   8. ]
 [ 0.1 -1.  -5. ]]

The above array has 2 dimensions. The first axis has a length of 2, the second axis has a length of 3. You can determine the shape/size/dimensionality of the area as follows:

print('Number of dimensions:', a.ndim)
print('Shape (length along each axis/dimension):', a.shape)
print('Size (total number of elements):', a.size)

Number of dimensions: 2
Shape (length along each axis/dimension): (2, 3)
Size (total number of elements): 6

Array Indexing: As in other programming languages, you can select specific elements from an array-or “index into the array” using square brackets as follows (note that arrays are zero-indexed):

print('Element at 0th row and 1st column =', a[0, 1])
print('Element at 1st row and 2nd column =', a[1, 2])

Element at 0th row and 1st column = 4.0
Element at 1st row and 2nd column = -5.0

You can also index into arrays in reverse order, meaning that we start from the end of the array. This is done using negative indexing as follows:

print('Element at 0th row and last column           =', a[0, -1])
print('Element at 1st row and second-to-last column =', a[1, -2])

Element at 0th row and last column           = 8.0
Element at 1st row and second-to-last column = -1.0

Array Types: Arrays can also store different types of elements (e.g. ints, floats, etc.). You can determine what type of elements they store as follows:

array_of_ints = jnp.array([1, 2, 3])
print('An array of ints has dtype:  ', array_of_ints.dtype)

array_of_floats = jnp.array([1.0, 2.0, 3.0])
print('An array of floats has dtype:', array_of_floats.dtype)

An array of ints has dtype:   int32
An array of floats has dtype: float32

Lastly, you can convert between array types as follows:

print('Array of ints converted to an array of floats:', array_of_ints.astype('float32'))

Array of ints converted to an array of floats: [1. 2. 3.]

2.3. Array Creation

There are several ways to create arrays. For example, you can create an array from a regular Python list or tuple using the jnp.array function. The type of the resulting array is deduced from the type of the elements in the sequences:

array_from_list = jnp.array([1.2, 3.5, 5.1])

The function jnp.zeros creates an array full of zeros, and the function jnp.ones creates an array full of ones. These functions all require the shape of the desired array. (Note that by default, the dtype of the created array is float64, but it can be specified via the keyword argument dtype).

array_of_zeros = jnp.zeros((3, 4))
print('Array of zeros:')
print(array_of_zeros)

Array of zeros:
[[0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]]

array_of_ones = jnp.ones((2, 3, 4))
print('Array of ones:')
print(array_of_ones)

Array of ones:
[[[1. 1. 1. 1.]
  [1. 1. 1. 1.]
  [1. 1. 1. 1.]]

 [[1. 1. 1. 1.]
  [1. 1. 1. 1.]
  [1. 1. 1. 1.]]]

To create sequences of numbers, we can use the jnp.arange function, which is analogous to the Python built-in range, but returns an array—by default, it counts from 0 up to the given number. A similar function you may want to check out is jnp.linspace.

print('From 0 to 10 in increments of 1:', jnp.arange(10.0))
print('From 4 to 20 in increments of 5:', jnp.arange(4.0, 20.0, 5.0))

From 0 to 10 in increments of 1: [0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]
From 4 to 20 in increments of 5: [ 4.  9. 14. 19.]

2.4. Shape Manipulation

Reshaping arrays: Sometimes you may find the need to change the shape of an array (while keeping its size the same). This can be done in a number of ways, depending on the need. First, you can simply reshape it:

a = jnp.arange(12)
print('a =', a)

a = [ 0  1  2  3  4  5  6  7  8  9 10 11]

print('a.reshape(3, 4) =')
print(a.reshape(3, 4))

a.reshape(3, 4) =
[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]

print('a.reshape(2, -1) =')
print(a.reshape(2, -1))

a.reshape(2, -1) =
[[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]]

In the above example, using the -1 argument tells reshape to automatically calculate the shape for that dimension.

Unsqueezing and Squeezing: Next, you may often find yourself needing to pad the dimension by 1—this is known as “unsqueezing.” By that, we mean that you may want to turn an array with shape \((N,)\) into an array with shape \((N, 1)\) or \((1, N)\). While under the hood, there’s really no difference between an \((N,)\)-shaped array and a \((N, 1)\)-shaped array—both contain \(N\) elements—there’s a practical difference between the two. Consider the following two examples:

• In ML, we often represent a data set of \(N\) observations, each \(D\)-dimensional, as an \((N, D)\)-array. To write generalizable code, it’s good to assume our data array therefore has two dimensions, even when \(D = 1\).

• When we want to concatenate several arrays together along a dimension they currently do not have. For example, we can concatenate two arrays of shape \((1, N)\) into a single array of \((2, N)\).

So how do we squeeze/unsqueeze in Jax? We can do it as follows:

# Create two arrays and print out their shape
a = jnp.arange(3)
b = jnp.arange(3) + 3
print('a       =', a)
print('b       =', b)
print('a.shape =', a.shape)
print('b.shape =', b.shape)

a       = [0 1 2]
b       = [3 4 5]
a.shape = (3,)
b.shape = (3,)

# "Unsqueeze" the array along it's 0-th axis
a_unsqueezed = a[None, ...]
b_unsqueezed = b[None, ...]
print('a_unsqueezed       =', a_unsqueezed)
print('a_unsqueezed.shape =', a_unsqueezed.shape)
print('b_unsqueezed       =', b_unsqueezed)
print('b_unsqueezed.shape =', b_unsqueezed.shape)

a_unsqueezed       = [[0 1 2]]
a_unsqueezed.shape = (1, 3)
b_unsqueezed       = [[3 4 5]]
b_unsqueezed.shape = (1, 3)

# Concatenate along its 0th axis
a_and_b = jnp.concatenate([a_unsqueezed, b_unsqueezed], axis=0)
print('a_and_b =')
print(a_and_b)
print('a_and_b.shape =', a_and_b.shape)

a_and_b =
[[0 1 2]
 [3 4 5]]
a_and_b.shape = (2, 3)

(We will explain what is meant by the ellipsis, ..., below). You can similarly take a way a dimension of size one by squeezing it: a_unsqueezed.squeeze(axis=1), where the axis argument tells us which dimension to remove.

2.5. Array Operations

Elementwise (shape-preserving) operations: Arithmetic operators on arrays apply elementwise. By this, we mean that the operation is applied independently to each element of the original array. A new array is then created and filled with the result.

# Create two arrays
a = jnp.array([20, 30, 40, 50]).astype('float32')
b = jnp.arange(4.0)
print('a =', a)
print('b =', b)

a = [20. 30. 40. 50.]
b = [0. 1. 2. 3.]

# When applied to a single array, operations apply to every element
print('b^2         =', b ** 2.0) # the double-star means power
print('10 * sin(a) =', 10.0 * jnp.sin(a))
print('a < 35      =', a < 35)

b^2         = [0. 1. 4. 9.]

10 * sin(a) = [ 9.129453  -9.880316   7.4511313 -2.6237485]
a < 35      = [ True  True False False]

# When applied to two arrays of the same shape, operations apply to corresponding elements 
print('a - b =', a - b)
print('a * b =', a * b)
print('b / a =', b / a)

a - b = [20. 29. 38. 47.]

a * b = [  0.  30.  80. 150.]

b / a = [0.         0.03333334 0.05       0.06      ]

All of the operations we showed above are element-wise operations, meaning that shapes of the inputs match the shapes of the outputs. Jax also has many useful operations that do not preserve the shape of the array. For example, an operation that computes a sum, minimum, or maximum, as follows:

a = jnp.arange(5.0)
print('a       =', a)
print('a.sum() =', a.sum())
print('a.min() =', a.min())
print('a.max() =', a.max())

a       = [0. 1. 2. 3. 4.]

a.sum() = 10.0
a.min() = 0.0

a.max() = 4.0

Non shape-preserving operations: Oftentimes, we will use these non-shape preserving operations on only one of the arrays dimensions. For these, we will need to specify the axis along which we would like to perform the operation. The axis is specified as a number, where, for 2-dimensional arrays, 0 means the operation will be performed over columns, and 1 means the operation will be performed over rows.

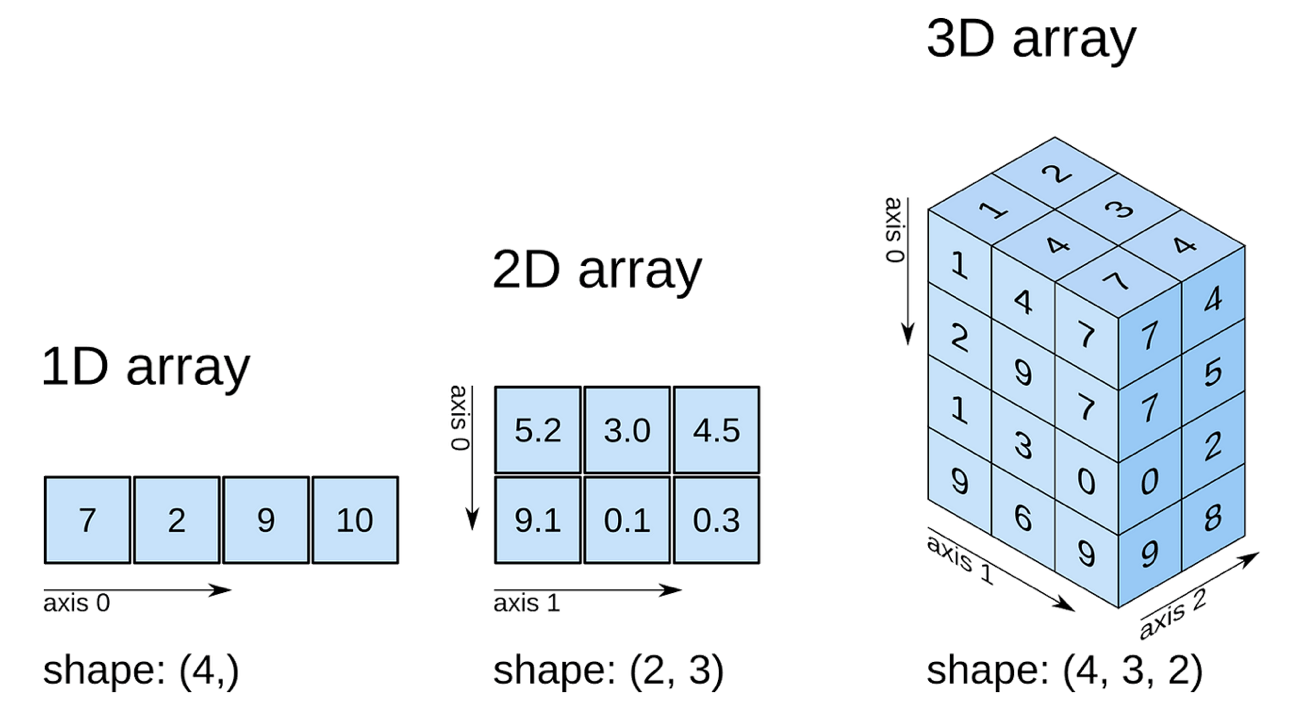
Fig. 2.1 Axes of arrays with different dimensions, taken from this tutorial.

Let’s illustrate this with some examples:

a = jnp.arange(12.0).reshape(3, 4)
print('a =')
print(a)

a =
[[ 0.  1.  2.  3.]
 [ 4.  5.  6.  7.]
 [ 8.  9. 10. 11.]]

print('a.sum(axis=0) =', a.sum(axis=0))
print('a.min(axis=1) =', a.min(axis=1))

a.sum(axis=0) = [12. 15. 18. 21.]
a.min(axis=1) = [0. 4. 8.]

Best practice for specifying axes: The axes can also be indexed in reverse, relative to the shape of the array. For example,

• For a 3-dimensional array with shape \((3, 4, 5)\), specifying axis=-1 means performing the operation on the dimension of size 5, resulting in a 2-dimensional array of shape \((3, 4)\).

• Similarly, specifying axis=-2 means performing the operation on the dimension of size 4, resulting in a 2-dimensional array of shape \((3, 5)\).

In NumPyro, which we will introduce later, it is best to always specify dimensions using the reverse/negative indexing.

What other operations exist in Jax? A lot. These are just a few examples. Any function you may be interested in likely already exists in Jax – be sure to look at the documentation (linked above) and google around before deciding to write your own!

Exercise: Array Operations

Please solve the following using Jax library calls only (no loops!):

Part 1: Write a function that, given \(N\), returns \(\sum\limits_{i=0}^{N - 1} \log(i + 1)\). Use the function signature below.

def array_operations_q1(N):
    pass # TODO implement

Test cases:

• For \(N = 10\), the result is \(15.104412\).

• For \(N = 20\), the result is \(42.335617\).

Part 2: Write a function that, given \(N\) and \(M\), returns \(\sum\limits_{i=0}^{N - 1} \sum\limits_{j=0}^{M - 1} \log(i \cdot j + 1)\). Use the function signature below.

def array_operations_q2(N, M):
    pass # TODO implement

Hint: one way to do this is with jnp.tile and jnp.transpose.

Test cases:

• For \(N = 5, M = 10\), the result is \(84.905975\).

• For \(N = 30, M = 20\), the result is \(2507.8206\).

Part 3: Implement a function that evaluates polynomials. That is, it takes in the degree of the polynomial, \(N\), an array of the \(N + 1\) coefficients, \(a\), a scaler \(x\), and evaluates:

\[\begin{align*} \sum\limits_{n=0}^N a_n \cdot x^{N - n}, \end{align*}\]

where \(a_n\) is the \(n\)th entry of array \(a\). Note, there exists a Jax function that does this—jnp.polyval. For the sake of the exercise, please don’t use it.

Test cases:

• For \(N = 3\), \(a = [1.0, -1.0, 0.0, 2.0]\), and \(x = 2.0\), the result is: \(6.0\).

• For \(N = 2\), \(a = [5.0, -2.0, 3.0]\), and \(x = 0.5\), the result is: \(3.25\).

Use the function signature below.

def array_operations_q3(N, M):
    pass # TODO implement

2.6. Array Slicing

Now that we have some general machinery for performing basic mathematical computation with arrays in Jax, we will introduce some ways of extracting subsections of arrays in different ways. We can do this as follows:

a = jnp.arange(10)
print('a =', a)

a = [0 1 2 3 4 5 6 7 8 9]

print('Everything until the 5th index           =', a[:5])
print('Everything from the 5th index onwards    =', a[5:])
print('Everything between the 2nd and 6th index =', a[2:6])
print('Everything except the last element       =', a[:-1])

Everything until the 5th index           = [0 1 2 3 4]
Everything from the 5th index onwards    = [5 6 7 8 9]
Everything between the 2nd and 6th index = [2 3 4 5]

Everything except the last element       = [0 1 2 3 4 5 6 7 8]

Of course, we can extend this to higher-dimensional arrays. First, note that a multi-dimensional array can be thought of as an array of arrays. That is, an array with shape \((N, M)\) can be thought of an array of length \(N\), in which every element is an array of length \(M\). Given this view, the notation we just introduced still works, it just returns 2-dimensional slices instead of 1-dimensional slices:

a = jnp.arange(15).reshape(5, 3)
print('a =')
print(a)

a =
[[ 0  1  2]
 [ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]
 [12 13 14]]

print('Everything until the 3th index =')
print(a[:3])

Everything until the 3th index =

[[0 1 2]
 [3 4 5]
 [6 7 8]]

print('Everything from the 3th index onwards =')
print(a[3:])

Everything from the 3th index onwards =
[[ 9 10 11]
 [12 13 14]]

print('Everything between the 1st and 3rd index =')
print(a[1:3])

Everything between the 1st and 3rd index =
[[3 4 5]
 [6 7 8]]

print('Everything except the last element =')
print(a[:-1])

Everything except the last element =
[[ 0  1  2]
 [ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]]

We can also slice arrays along multiple dimensions simultaneously:

a = jnp.arange(15).reshape(5, 3)
print('a =')
print(a)

a =
[[ 0  1  2]
 [ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]
 [12 13 14]]

print('Example: slicing each axis differently =')
print(a[:3, 1:])

Example: slicing each axis differently =
[[1 2]
 [4 5]
 [7 8]]

print('Example: slicing only the second axis =')
print(a[:, 1:])

Example: slicing only the second axis =

[[ 1  2]
 [ 4  5]
 [ 7  8]
 [10 11]
 [13 14]]

Notice in the above, : indicates “take everything along axis”.

Last but not least, we introduce the elipsis notation you saw earlier (when squeezing and unsqueezing): .... This notation is similar to :. It says “take everything along all axes up until current axis.” This might be confusing, so let’s illustrate this with an example. Suppose we have an array a of shape \((N, M, K, L)\):

• a[..., :5] will return an array of size \((N, M, K, 5)\). It leaves all axes alone except the very last one, from which it keeps only the first 5 entries.

• Similarly, a[..., :3, :5] will return an array of size \((N, M, 3, 5)\).

• We can also put the elipsis at the end. a[:-2, ...] will return an array of size \((N - 2, M, K, L)\).

Exercise: Array Slicing

Please solve the following using Jax library calls only (no loops!): Part 1: Write a function that, given an array a of shape \((N,)\), returns a new array b of shape \((N - 1,)\) in which index \(i\) contains b[i] = a[i + 1] - a[i].

For example, given, a = jnp.array([0.0, 1.0, 5.0, 10.0, 20.0]), the function should return Array([ 1.,  4.,  5., 10.], dtype=float32).

Use the following function signature:

def array_slicing_q1(a):
    pass # TODO implement

Part 2: Extend the function you wrote to multi-dimensional arrays, where the operation is only performed on the last dimension. That is, if an array a of shape \((N, M, K)\) is given, return an array b of shape \((N, M, K-1)\).

For example, given,

a = jnp.array([
    [0.0, 1.0, 5.0, 10.0, 20.0],
    [2.0, 5.0, 6.0, 20.0, 30.0],
])

the function should return,

Array([[ 1.,  4.,  5., 10.],
       [ 3.,  1., 14., 10.]], dtype=float32)

Use the following function signature:

def array_slicing_q2(a):
    pass # TODO implement