13. Regression#
# Import some helper functions (please ignore this!)
from utils import *
Context: At this point, you have the building blocks for developing many commonly-used ML models. Using these building blocks, we will develop a commonly used ML model—regression. A regression model is a predictive model (i.e. a conditional distribution), in which the variable we’re interested in predicting is a real number.
Challenge: Recall that in a conditional distribution, the parameters of the distribution depend on what we’re conditioning. For example, when predicting the probability of intoxication, \(I\), given the day of the week, \(D\), we can use a model like,
where the parameter, \(\rho(d)\), is a function of the condition (i.e. the day \(d\)):
As in this model, in all models we’ve considered so far, the parameters depend on the condition using if-else expressions (e.g. if \(d\) is a weekday, then \(\rho = 0.1\), else \(\rho = 0.4\)). Unfortunately, as models become more complex, this approach for specifying a model becomes unwieldy. For example, if instead of conditioning on something simple, like the day, we instead conditioned on something complicated, like medical image—\(1000 \times 1000\) pixels in size—how would we write the appropriate if-else expression? Out of a total of 1-million pixels in the image, which ones are important to even include in the if-else expression? The classes of predictive models we will introduce now—regression and (later) classification—precisely allow us to circumvent this issue. How? By making the parameter a more interesting function of the condition. Continuing with the above example, we can define, \(\rho(d)\) as a linear function of \(d\):
We can similarly make \(\rho(d)\) a quadratic, or sinusoidal, or polynomial function of \(d\)—there are endless possibilities. Of course, in this example, \(d\) can be one of two values, so making \(\rho(d)\) some function of \(d\) is not helpful—but when \(d\) is more complicated, like an image, this trick will be incredibly helpful. We will start with simple, linear functions, and build up to more complex functions (using neural networks).
Outline:
Introduce predictive models generally
Instantiate a regression model as a specific type of predictive model
Implement the regression in
NumPyroUnderstand correlation vs causation
Relate to non-probabilistic regression
Data: Before diving in, let’s familiarize ourself with the data set we’ll be working with. This data set comes from a special, interdisciplinary effort at the IHH, spanning two major centers. The first is one you’re already familiar with: the Center for Telekinesis Research (CTR), dedicated to the study of telekinesis (the ability of moving physical objects with your mind). The second is the Center for Glow and Positive Life Flow (CGLF). As you know, one of the great mysteries of the galaxy is why intergalactic beings glow, and what it can tell us about other aspects of their life. As part of this effort, IHH researchers want to understand how glow affects telekinetic ability. They have recruited you to help with the data analysis.
They sent us a data set consisting of two variables:
A measure of glow (real number), in which higher values indicate higher brightness
A measure of telekinetic ability (also real number), in which higher values indicate higher ability (able to move heavier objects to greater heights, etc.)
# Import a bunch of libraries we'll be using below
import pandas as pd
import matplotlib.pylab as plt
import numpyro
import numpyro.distributions as D
import jax
import jax.numpy as jnp
# Load the data into a pandas dataframe
csv_fname = 'data/IHH-CTR-CGLF-regression.csv'
data = pd.read_csv(csv_fname, index_col='Patient ID')
# Print a random sample of patients, just to see what's in the data
data.sample(15, random_state=0)
| Glow | Telekinetic-Ability | |
|---|---|---|
| Patient ID | ||
| 90 | 0.604085 | -0.020933 |
| 254 | 0.613645 | -0.070165 |
| 283 | 0.829212 | 0.140791 |
| 445 | 0.981120 | 0.261027 |
| 461 | 0.688329 | -0.027250 |
| 15 | 0.796853 | -0.033701 |
| 316 | 0.839546 | 0.344510 |
| 489 | 0.929422 | 0.268031 |
| 159 | 0.893813 | 0.422464 |
| 153 | 0.832483 | 0.375658 |
| 241 | 0.676760 | -0.028127 |
| 250 | 0.711121 | -0.078376 |
| 390 | 0.683075 | 0.176542 |
| 289 | 0.472696 | -0.153246 |
| 171 | 0.703657 | 0.028212 |
fig, ax = plt.subplots(1, 1, figsize=(6, 4))
plt.scatter(data['Glow'], data['Telekinetic-Ability'], color='red', alpha=0.5)
plt.xlabel('Glow')
plt.ylabel('Telekinetic Ability')
plt.title('Telekinetic Ability vs. Glow')
plt.tight_layout()
plt.show()
13.1. Predictive Models#
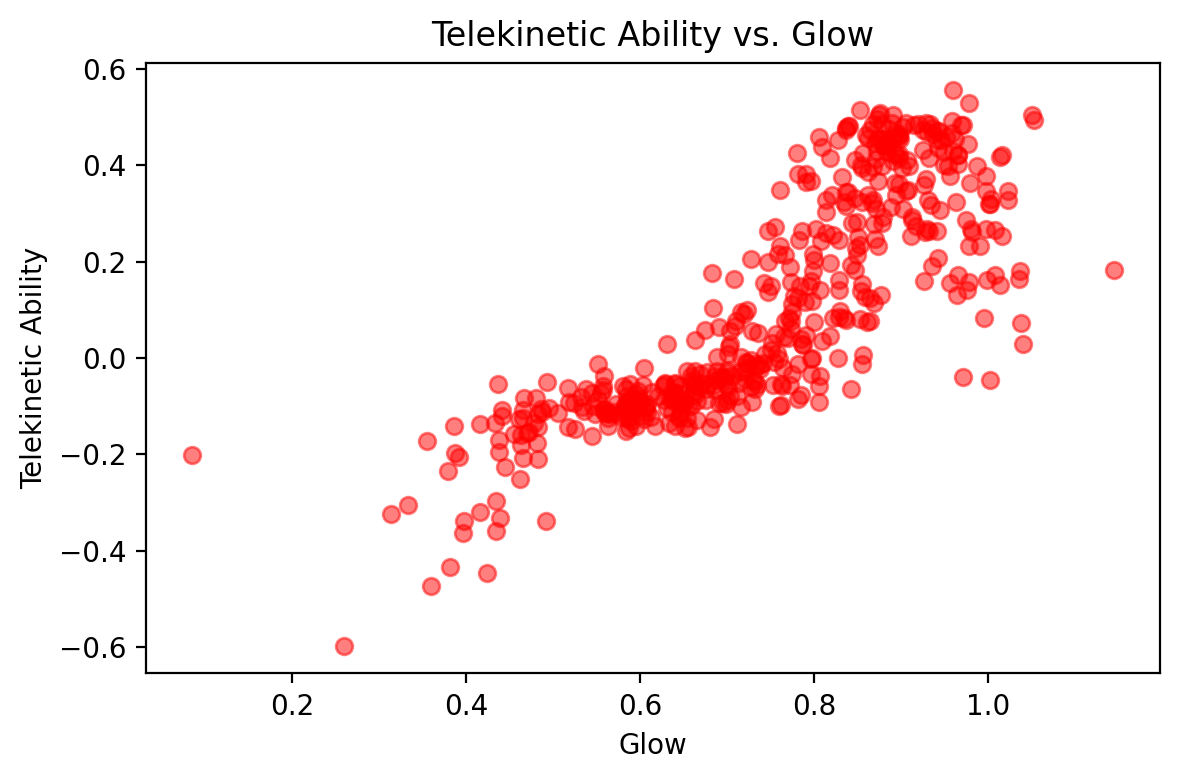
To understand the effects of glow on telekinetic ability, we will try to see if there is a relationship between them—if glow changes, does telekinetic ability change as well? To do this, we will fit a predictive model (and more specifically, a regression model) to the data. We will then interpret it and see what we learn. Of course, we have to be cautious about our interpretation of the results: just because telekinetic ability may change as a function of glow does not mean that it causes the change—more on that later.
Approach. Since regression models are a specific type of predictive model, let’s first describe what a predictive model is using the toolkit we’ve developed so far. Specifically, we’ll describe a predictive model using the directed graphical model and its corresponding generative process. Then, we will write down its joint data distribution and MLE objective.
Directed Graphical Model. We have data set of observations of two RVs: “inputs” \(X\), representing glow, and “outputs” \(Y\), representing telekinetic ability. Our goal is to learn to predict \(Y\) from \(X\) (i.e. learn a conditional distribution \(p_{Y | X}\)). Our graphical model should therefore include the following:
It should have a node for \(X\) and a node for \(Y\), representing our two random variables.
It should have an arrow pointing from \(X\) into \(Y\) to represent \(Y\)’s dependence on \(X\).
Since we have many i.i.d observations of \((X, Y)\)-pairs, we’ll need \(X\) and \(Y\) in a plate.
Finally, the we’ll probably want the relationship between \(X\) and \(Y\) to be controlled by some parameter, \(\theta\), that can be learned from the data.
A predictive model has the following graphical representation:
Generative Process. Our graphical model can be directly translated into the following generative process: for \(n = 1, \dots, N\),
Notice that we’ve chosen our marginal over the inputs, \(p_X(x_n)\), to not depend on any parameters. This is because we just care about learning how to predict \(Y\) from \(X\). That is, we assume our use-case will be that we are given specific \(x\)’s for which we want to make predictions—we therefore don’t need to sample them from \(p_X(\cdot)\) (or learn \(p_X(\cdot)\)). As you will see in the derivation of our objective function, \(p_X(x_n)\) will not impact our MLE in any way.
Joint Data Log-Likelihood. For the above model, we have the following joint data log-likelihood:
MLE Objective. Our goal is to maximize the probability of the joint data log-likelihood with respect to parameters \(\theta\):
This gives us the following objective (or loss function):
Now that we have our objective, the only thing missing now is a specific choice of \(p_{Y | X}(y_n | x_n; \theta)\); given a specific value of glow, \(x_n\), what’s the distribution of telekinetic ability, \(y_n\)? We will next select \(p_{Y | X}(y_n | x_n; \theta)\) to give us a regression model. Later, we will do the same for other models (e.g. classification).
13.2. The Regression Model#
The Model. Looking at our objective function, \(\mathcal{L}(\theta)\), the only thing we need to define is \(p_{Y | X}(y_n | x_n; \theta)\). Let’s introduce a picture to help our intuition for what this distribution should be. Looking at the plot above of telekinetic ability vs. glow, we see that \(p_{Y | X}(y_n | x_n; \theta)\), should have two parts:
It needs some way of accounting for the general “trend”. As glow increases, telekinetic ability also increases until the very end, when it drops off.
Around this trend, there is some “noise”—no point exactly fits the trend.
To capture both components, we define our model as follows:
where \(\theta = \{ W, \sigma \}\), and where \(\mu(\cdot; W)\) is a function parameterized by \(W\) (which controls its shape). Putting this all together, our generative process says:
We’re given an input, \(x_n\), from our data.
We feed it through our function \(\mu(\cdot; W)\) to predict what \(y_n\) will be, on average. This captures the “trend.”
Finally, we add some Gaussian noise to the result. This Gaussian noise represents the error in our measurement. For example, our devices that measure height, blood pressure, etc. at the IHH are correct on average, but are always off by some small amount of random noise. How much noise is determining by the variance of the Gaussian, \(\sigma^2\).
Expressivity. Let’s visualize what this looks like:
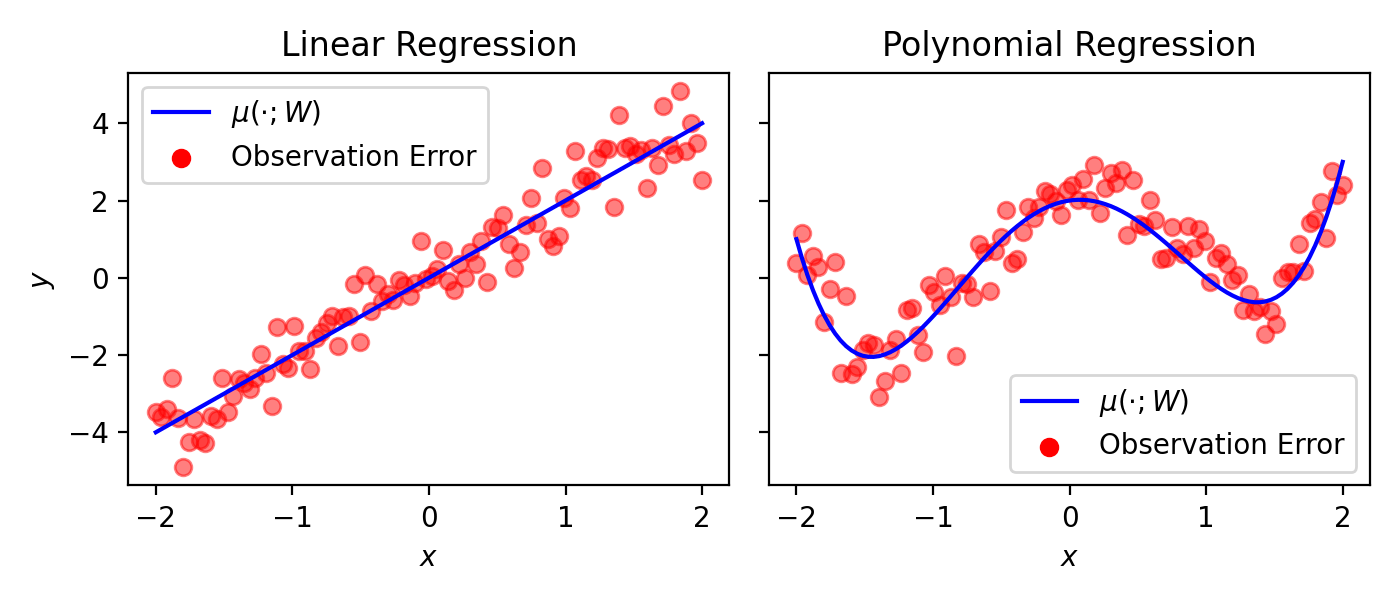
Fig. 13.1 Examples of regression with linear \(\mu(\cdot; W)\) (left) and polynomial \(\mu(\cdot; W)\) (right).#
Here, the blue line, representing \(\mu(\cdot; W)\) captures the “trend” of the data. The data (in red) surrounds the trend; it lies around it due to the observation error (or noise). In the “linear” regression plot, \(\mu(x_n; W)\) is a line, where \(W = \{ a, b \}\) is the slope and intercept of a line:
In the “polynomial” regression plot, \(\mu(x_n; W)\) is a polynomial function of \(x_n\), where \(W = \{ a, b, c, d, e \}\) captures the coefficients of the polynomial:
13.3. Implementing Regression Models in NumPyro#
Exercise: Implement Linear Regression
Part 1: Using NumPyro, implement a linear regression model. Your model should only include the conditional distribution of telekinetic ability given glow; it should not include the marginal distribution of glow. Your model should therefore have the following signature:
def model_linear_regressor(N, x, y=None):
pass # TODO implement
Notice that here, we expect \(x\) / glow to always be passed in. This is because we’re not looking to learn the distribution of glow—we’re always going to be given it.
Part 2: Fit the model to the data using the MLE. Plot the loss and verify that your optimization converged. In your plot you may want to zoom in on the last iterations of optimizations to verify it indeed converged.
Part 3: Visualize your model fit by plotting samples from your model against the real data.
How well does your model fit the data?
For what patients will it perform well, and for which patients will it perform badly?
Exercise: Implement Polynomial Regression
Part 1: Using NumPyro, implement polynomial regression. Your model will now take one additional argument—the degree of the polynomial (a polynomial in which the highest term is \(x^4\) is of degree \(4\)). Please use the function signature below. You can use jnp.polyval.
def model_polynomial_regressor(N, x, y=None, degree=1):
pass # TODO implement
Part 2: Fit the model to the data using the MLE with degree=2, 5 and 8. For each, plot the loss and verify that your optimization converged.
Part 3: Answer the following questions.
How well does each model fit the data?
Which model would you ultimately recommend to the researchers at the IHH? Why? Your answer should look at how the model interpolates, meaning the trend it learns for the points in your data, and also how it extrapolates, meaning the trend it learns away from your data (e.g. in the extreme values of the inputs).
13.4. Correlation vs. Causation#
Exercise: Correlation vs. Causation
Now that you have several models that reasonably fit the data, you have a meeting scheduled with the IHH researchers from the Center for Telekinesis Research and the Center for Glow and Positive Life Flow. In the meeting, you will discuss the results of the modeling and try to determine what scientific insights you can gather.
Part 1: Just based on the analysis you’ve conducted so far, do you think a brighter glow causes heightened telekinetic ability? Do you think a heightened telekinetic ability causes a brighter glow? Or neither? Why?
Part 2: After much deliberation, the other IHH researchers mention that since they’ve given you the data, they’ve collected some additional variables. They send you their new, augmented data set, which can be found at data/IHH-CTR-CGLF-regression-augmented.csv. Load the data in and create scatter plots of the relationship between every pair of variables. Does this data set offer another potential explanation for the relationships between glow and telekinetic ability?
Part 3: As the augmented data shows, instead of a brighter glow causing heightened telekinetic ability, there is a third variable that actually explains this relationship. This variable is called a “confounding variable”—a variable that explains what we perceive to be the cause and its effect. In the following examples, identify the confounder and use it to explain why the initial conclusions are wrong.
When ice cream sales increase, so do wildfires. Therefore, we should ban ice cream to prevent wildfires.
As the number of CS and DS faculty Wellesley hires increases, so does the level of the ocean. Therefore, by decreasing the size of Wellesley’s CS and DS departments, we can lower rising ocean levels.
As the number of pirates decreases, the average temperature of the earth increases. Therefore, we need to bring back pirates to reduce global warming.
Browse this website, which presents a variety of spurious correlations. Pick one and explain it.
Part 4: In performing data analysis like the types of analyses covered here, we are always at risk of drawing wrong conclusions.
What are the pitfalls we might fall into?
In this specific instance, what are the implications of reaching the wrong conclusion?
How can you avoid these pitfalls?
13.5. Comparison with Non-Probabilistic Regression#
Non-Probabilistic Regression. In non-probabilistic approaches to ML, one typically writes down a loss function directly (without necessarily deriving it from the MLE of the model). Specifically, one typically choses some notion of prediction error they want to minimize, and write down an objective to minimize it directly. A common choice of loss function for regression is minimizing the mean squared error (MSE).
As you can see in the loss function above, we have some function, \(\mu(x_n; W)\), that aims to predict \(y_n\). Our goal is to minimize the square error between the predictor and \(y_n\), averaged across our whole data set. Of course, we can pick any notion of error we want, but what’s interesting is that different choices of error implicitly define a probabilistic model.
Relating MSE-Loss to Gaussian Observation Error. We will now show how finding a \(W\) that minimizes the MSE-loss is equivalent to finding a \(W\) via the MLE. Here, we will only minimize our objective relative to \(W\) (ignoring \(\sigma\)). We start with the MLE objective for our regression model from above:
As you can see, both the probabilistic and non-probabilistic formulations yield the same \(W\).
Why use the probabilistic approach? The probabilistic approach forces us to spell out our assumptions in the form of a model. It forces to spell out exactly which variables depend on which other variables (via a directed graphical model), and what is the nature of the dependence (when selecting specific distributions and parameterizations for functions). As such, when our model fits the data poorly, the probabilistic approach allows us to investigate why. For example, you may have noticed that none of the models you developed to predict telekinetic ability from glow fit the data perfectly. Why is that? Let’s investigate.
Exercise: Diagnosing Model Mismatch
Pick one of the models you’ve fit to the data above. For the model you chose, plot the distribution of observation errors using a histogram. That is, plot the distribution of \(y_n - \mu(x_n; W^\text{MLE})\)—these are called “residuals.”
Given our modeling assumptions, what should this distribution be? How do you know?
Does the distribution we observe empirically match the distribution from our model? Why?
Hint: You can estimate \(\mu(x_n; W^\text{MLE})\) using the mean of \(y \sim p_{Y|X}\).
Conclusion. There are two important bits we want you to take away from this last part:
The derivation above that equates Gaussian observation noise with MSE-loss points to the importance of our modeling assumptions. For example, each choice of observation noise distribution implies a different notion of “error” between our trend \(\mu(\cdot; W)\) and \(y\). It’s therefore important to pick distributions that are both informed by domain knowledge and by the data.
While for the types of predictive models we introduce here, both the probabilistic and the non-probabilistic approaches may yield the same predictor, the probabilistic approach offers an important advantage. It allows us to interrogate why a model fits poorly. This is, of course, not the only advantage of the probabilistic paradigm! We will soon get to more things you can do with it that you cannot do with the non-probabilistic paradigm.
