11. Probability (Continuous)

# Import some helper functions (please ignore this!)
from utils import * 

Context: Many real-world data sets include non-discrete values (e.g. a patient’s body-mass index (BMI), the dosage of medicine, and more). Here, we will introduce what you need to know in order to model continuous-valued data.

Challenge: In many ways, continuous probability is similar to discrete probability. However, there are a few “gotchas” that are important to highlight.

Outline:

• Introduce and practice the concepts, terminology, and notation behind continuous probability distributions.

• Gain familiarity with several common continuous distributions.

11.1. Differences Between Continuous and Discrete Probability

Continuous probability functions the same way as discrete probability, except for a few key differences.

Sample Space of Support: The support of continuous probability distributions is over “uncountably infinite sets.” If you’re not familiar with this term, that’s ok! In this course, we’ll think about it more as a distribution supported over the real numbers, \(\mathbb{R}\) (or some subset thereof).

Example: Let \(H\) be a continuous RV, describing the distribution of heights in the IHH ER. The support of \(H\) is the interval \((0, \infty)\) on the real line.

Probability Mass Function (PMF): Continuous probability distributions DO NOT have PMFs; this is because, unlike discrete distributions, we cannot think of continuous distributions in terms of frequency. Let’s illustrate this with an example.

Example: Suppose we are modeling the probability of intoxication as a Bernoulli RV, \(I\). If we say that the probability of intoxication (or \(I=1\)) is \(0.5\) (meaning \(p_I(1) = 0.5\)), meaning half of our patients will have intoxication. Such a statement about the PMF of a discrete distribution can be immediately translated into intuition about frequency. On the other hand, suppose we have a continuous RV, \(H\), modeling the height of patients. How can we describe the probability that a patient is 50 inches tall (i.e. what is \(p_H(50)\)?). Let’s try to get some intuition. Of the patients in the data, maybe we have one that’s \(50.1\) inches tall, another that is \(49.9\), or maybe one that’s \(49.999991\) inches tall—but what are the chances we will observe a patient that is exactly (not approximately) \(50\) inches tall? The answer is: zero. This is because of the arbitrary precision we have on continuous values. So if we can’t describe continuous distributions using PMFs, how else can we describe them? As you will see next, we will have to use a more circuitous route.

Exercise: Why continuous distributions do not have PMFs

Demonstrate empirically that continuous distributions do not have valid PMFs via the following procedure:

1. Sample 10,000 values from a Uniform distribution on the range \([0, 1]\) (using NumPyro). This will draw samples on the range \([0, 1]\) with equal probability.

2. Count the number of samples that exactly equal \(0.5\). How many samples did you count?

Cumulative Density Function (CDF): As we showed, we can’t use the frequency of a continuous RV as its probability. But we can ask a different question: what’s the probability that a continuous RV is smaller than or equal to some value. This is called the CDF, which we will denote using \(F\). What’s interesting about the CDF is that it abides by our intuition of probability as frequencies; we can empirically estimate the CDF by counting all samples for which the variable is \(\leq\) our value of interest. Next, we will use the CDF to define the “continuous RV version” of the PMF. Before moving on, however, let’s illustrate this by continuing with our example of IHH ER patient height.

Example: Let \(F_H(\cdot)\) define the CDF of a continuous RV, \(H\), describing the height of IHH ER patients. We use \(F_H(h)\) to denote the probability that the height \(H\) is smaller than some specific value, \(h\) (e.g. \(F_H(50)\) is the probability that the patient’s height is \(\leq 50\)). To evaluate \(F_H(50)\) from data, we can simply look at the frequency of patients for which \(H \leq 50\), just as we did with discrete probability!

Properties of CDFs: Let \(R\) be an RV with CDF \(F_R(\cdot)\).

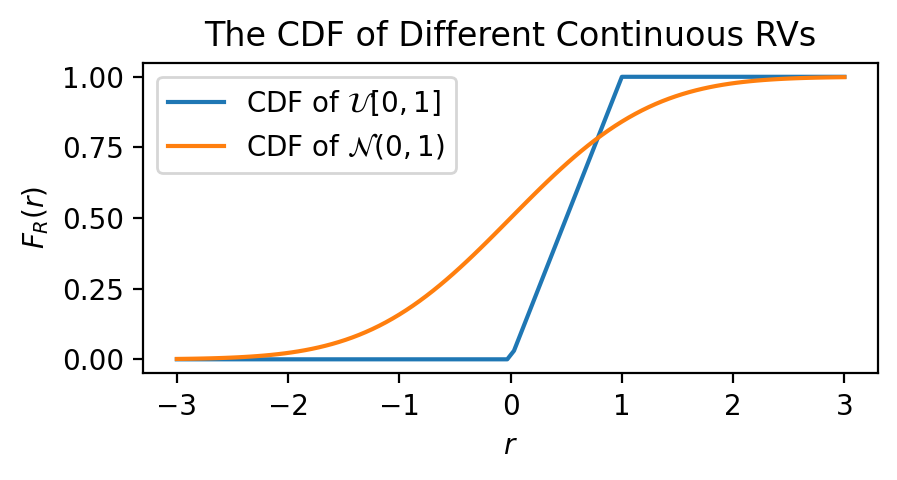
1. The CDF is non-decreasing. When \(r_1 < r_2\), we also have that \(F_R(r_1) \leq F_R(r_2)\).

   Example: Continuing with our running example, the probability that height is smaller than 50 inches is smaller or equal to the probability that height is smaller than 60 inches: \(F_H(50) \leq F_H(60)\). This is because the number of patients with \(H \leq 60\) should be \(\geq\) the number of patients with \(H \leq 50\).

2. The CDF is bounded by \(0\) below and by \(1\) above. Let \(L\) and \(U\) be the smallest and largest values in the sample space, respectively. Then, \(\lim\limits_{r \rightarrow L} F_R(r) = 0\), and \(\lim\limits_{r \rightarrow U} F_R(r) = 1\).

   Example: In our running example, \(L = 0\) (people must have a positive height) and \(U = \infty\) (they can be arbitrarily tall). We denote \(\lim\limits_{h \rightarrow 0} F_H(h)\) as the probability that a patient’s height is \(\leq 0\). Since a patient can’t be 0 inches or less, this limit evaluates to \(0\). Similarly, \(\lim\limits_{h \rightarrow \infty} F_H(h)\) denotes the probability that a patient’s height is smaller than infinity. Since this is always true, this limit evaluates to \(1\).

We will now plot the CDF of some different continuous RVs (a uniform distribution and a normal distribution, denoted by \(\mathcal{U}\) and \(\mathcal{N}\), respectively). Can you check that both properties are satisfied?

import numpyro
import numpyro.distributions as D

fig, ax = plt.subplots(1, 1, figsize=(4.5, 2.5))

r = jnp.linspace(-3.0, 3.0, 100)
plt.plot(r, D.Uniform().cdf(r), label=r'CDF of $\mathcal{U}[0, 1]$')
plt.plot(r, D.Normal().cdf(r), label=r'CDF of $\mathcal{N}(0, 1)$')

plt.xlabel('$r$')
plt.ylabel('$F_R(r)$')
plt.title('The CDF of Different Continuous RVs')
plt.legend()
plt.tight_layout()
plt.show()

Probability Density Function (PDF): We will now introduce the PDF—the “continuous RV version of the PMF”—using the CDF. To do this, we will introduce just one more fact about the CDF. This fact will allow us to compute the probability of an RV lying between two values: suppose we have a continuous RV, \(R\) with CDF \(F_R(\cdot)\), then the probability that \(l < R \leq u\) is given by \(F_R(u) - F_R(l)\).

Example: Suppose we want to know the probability that a patient’s height is between \(40\) and \(60\) inches. Let’s start by computing the probability that the patient’s height is less than \(60\) inches—but this also includes patients whose height is also less than \(40\) inches (which we want to exclude). To do this, we can subtract the probability that their height is less than \(40\) inches. This gives us \(F_H(60) - F_H(40)\).

Using our new fact, let’s set up the problem differently. Instead of trying to directly compute the probability of \(R = r\) (which is always 0), let’s compute the probability that \(R\) is super close to \(r\). We can do this by making up a variable, \(\epsilon\), that is very small, and computing how the CDF changes from \(F_R(r - \epsilon)\) to \(F_R(r)\). In other words, we want the instantaneous rate-of-change from \(F_R(r - \epsilon)\) to \(F_R(r)\), since this rate-of-chance can be thought of as “the inclusion of \(r\)”.

Now, the instantaneous rate-of-change is also known as the derivative. Thus, we define the PDF as the derivative of the CDF:

(11.1)\[\begin{align} p_R(r) &= \frac{d F_R(r)}{d r}. \end{align}\]

Properties of PDFs: Let \(R\) be a continuous RV with PDF \(p_R(\cdot)\), defined on the sample-space \(S\).

1. The PDF must integrate to 1. That is, \(\int\limits_{r \in S} p_R(r) dr = 1\). This is analogous to the fact that discrete probabilities must sum to 1.

   Example: If \(R\) is drawn from a Normal distribution, then our sample space is \(S = (-\infty, \infty)\). We must therefore have that \(\int\limits_{-\infty}^\infty p_R(r) dr = 1\).

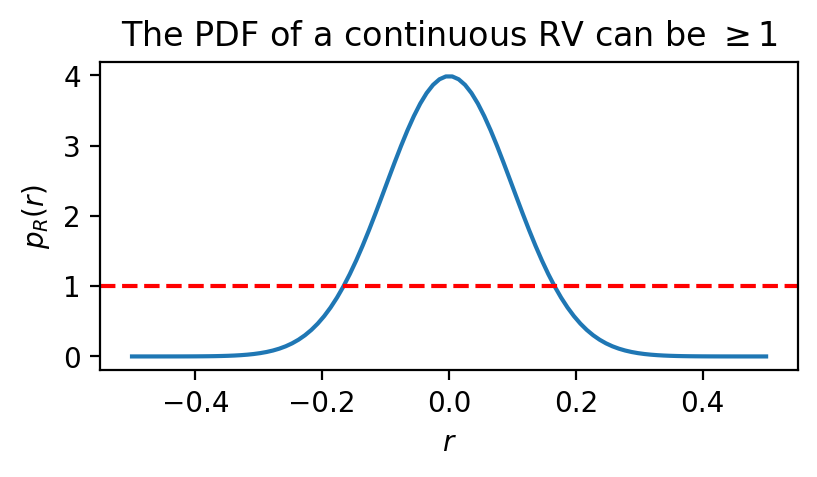
2. The PDF can be greater than 1. This is in contrast to discrete probability, in which the PMF can never be greater than 1.

   Example: Examine the plot of the PDF of the normal distribution (with parameters of \(\mu = 0\) and \(\sigma = 0.1\)) below. Notice that it rises above 1.

fig, ax = plt.subplots(1, 1, figsize=(4.5, 2))

r = jnp.linspace(-0.5, 0.5, 100)
plt.plot(r, jnp.exp(D.Normal(0.0, 0.1).log_prob(r)))
plt.axhline(1.0, color='red', ls='--')

plt.xlabel(r'$r$')
plt.ylabel(r'$p_R(r)$')
plt.title(r'The PDF of a continuous RV can be $\geq 1$')
plt.show()

Exercise: Gaining comfort with commonly-used continuous distributions

Browse the Wikipedia pages for the following distributions:

• Uniform

• Beta

• Normal (or Gaussian)

• Truncated Normal

• Laplace

Part 1: For each of the distributions above, plot its PDF (using NumPyro). Play with the parameters of each distribution—how does each affect the shape of the distribution? Summarize what you learn.

Part 2: Answer the following questions:

1. You’re modeling the distribution of heights in the US. Which of the above distributions would you choose and why?

2. You have a large collection of antique coins. Unlike modern-day coins, your coins don’t have a 50% probability of landing heads. You’re interested in modeling the distribution of the probability of them landing heads. That is, each coin has a different probability of landing heads—you want to model the distribution of these probabilities. Which of the above distributions would you choose and why?

3. You’ve been given a prototype of a new sensor that determines the location of the nearest intergalactic being. The sensor is, on average, correct, but is typically a little off (sometimes it overshoots and sometimes it undershoots the location). Which of the above distributions would you use to describe the error and why?

Hint: On each Wikipedia page, there’s a panel on the right side that summarizes the properties of the distribution (e.g. its support, PDF, example plots, etc.)—all of the information you need is there.

11.2. Expectations

An expectation, or expected value, is a fancy name for an average (or mean). As you may have noticed, the parameters for several of the distributions above control their mean (e.g. for a Gaussian and Laplace). This is useful for modeling since it allows us to specify what the model should do “on average.” Expectations will also keep popping up in later derivations—so what are they exactly?

Approximating Expectations. Given samples from an RV, you likely know how to compute the average: you add up all of the samples and divide by the total number of samples. For example, let \(N\) be an RV representing the number of presents a person gets for their birthday. You can approximate the expectation/average, by:

1. Randomly selecting \(S\) individuals from the population

2. Asking each for the number of presents they got, \(n_s\),

3. Computing the average via,

\[\begin{align*} \underbrace{\mathbb{E}_{n \sim p_N(\cdot)} [n]}_{\text{fancy notation}} &\approx \underbrace{\frac{1}{S} \sum_{s=1}^S n_s}_{\text{average}}, \text{ where, } n_s \sim p_N(\cdot). \end{align*}\]

You can expect that for a large \(S\), this approximation will be close to the true average.

In the fancy notation above,

• \(\mathbb{E}\) denotes “expectation.”

• The subscript, \(n \sim p_N(\cdot)\), denotes the random variable we’re drawing. In this case, it’s the number of birthday presents.

• \(n\), surrounded by the brackets, is the thing we’re averaging. If we knew each present cost 10 USD, and if we wanted to approximate the average cost, we can replace \(n\) with \(10.0 \cdot n\).

Defining Expectations. Suppose we have a discrete RV, \(A\), with PMF \(p_A(\cdot)\), and that we want to compute the expected value of \(f(a)\), where \(a \sim p_A(\cdot)\). Then:

(11.2)\[\begin{align} \mathbb{E}_{a \sim p_A(\cdot)} [f(a)] &= \sum_{a \in S} p_A(a) \cdot f(a). \end{align}\]

If \(A\) were a continuous RV, we replace the sum in the above definition with an integral:

(11.3)\[\begin{align} \mathbb{E}_{a \sim p_A(\cdot)} [f(a)] &= \int_{a \in S} p_A(a) \cdot f(a) \cdot da. \end{align}\]

So where did these formulas come from? And how do they relate to our approximation? Let’s return to our birthday present example. We re-order our samples, \(n_s\), in ascending order, from least to most number of birthday presents, and see the following pattern:

• 2 people received 0 presents

• 3 people received 1 present

• 4 people received 2 presents

• 1 person received 3 presents

• 0 people received 4 or more presents

Plugging this into our approximation formula above, we have:

\[\begin{align*} \mathbb{E}_{n \sim p_N(\cdot)} [n] &= \sum_{n=1}^\infty p_N(n) \cdot n \\ &\approx \frac{1}{S} \sum_{s=1}^S n_s \\ &= \frac{1}{S} ( 0 + 0 + 1 + 1 + 1 + 2 + 2 + 2 + 2 + 3 + 0 \cdot 4 ) \end{align*}\]

We can then aggregate the numbers as follows, and distribute the division by \(S\):

\[\begin{align*} &= \frac{1}{S} ( 2 \cdot 0 + 3 \cdot 1 + 4 \cdot 2 + 1 \cdot 3 + 0 \cdot 4 ) \\ &= \frac{2}{S} \cdot 0 + \frac{3}{S} \cdot 1 + \frac{4}{S} \cdot 2 + \frac{1}{S} \cdot 3 + \frac{0}{S} \cdot 4 \\ &= \sum_{n=1}^\infty \underbrace{\frac{\text{number of people who got $n$ presents}}{\text{number of people sampled}}}_{\text{Approaches $p_N(n)$ as $S \rightarrow \infty$}} \cdot n, \end{align*}\]

which is our definition of expectation.

11.3. MLE for Discrete-Continuous Models

You’ve recently been contacted by researchers at the IHH’s Center for Telekinesis Research (CTR). The researchers at the IHH’s CTR study the propensity of intergalactic beings for telekinesis—the ability of moving physical objects with their mind (how cool!). At the moment, they are interested in understanding how different physiological conditions affect a being’s telekinetic abilities (measured as a real number, with larger numbers indicating heightened telekinetic abilities). They have collected the following data sets and would like your help in analyzing it. Let’s load it and have a look!

# Import a bunch of libraries we'll be using below
import pandas as pd
import matplotlib.pylab as plt

# Load the data into a pandas dataframe
csv_fname = 'data/IHH-CTR.csv'
data = pd.read_csv(csv_fname, index_col='Patient ID')

# Print a random sample of patients, just to see what's in the data
data.sample(15, random_state=0)

	Condition	Telekinetic-Ability
Patient ID
398	Allergic Reaction	0.510423
3833	Allergic Reaction	0.479960
4836	Intoxication	2.043218
4572	Allergic Reaction	-0.443333
636	Intoxication	1.423190
2545	Intoxication	1.392568
1161	Intoxication	2.110151
2230	Intoxication	2.102866
148	Intoxication	1.865081
2530	Allergic Reaction	0.401414
4070	Intoxication	2.271342
1261	Allergic Reaction	-0.455159
4682	Entangled Antennas	-1.713834
333	Intoxication	2.000120
906	Intoxication	1.693633

Exercise: Modeling Data from the IHH’s Center for Telekinesis Research

Let \(C\) and \(A\) denote the RVs representing “Condition” and “Telekinetic-Ability,” respectively. Your goal is to learn a generative model (i.e. a joint distribution) of \(A\) and \(C\).

Part 1: Let’s first perform an exploratory data analysis.

• Visualize the marginals, \(p_C(\cdot)\) and \(p_A(\cdot)\).

• Visualize the conditional \(p_{A | C}(\cdot | c)\) for every value of \(c\).

• Can you visualize \(p_{C | A}(c | a)\)? Explain what makes this challenging.

Part 2: Based on the visualizations, which of the following factorizations of the joint would you prefer to use? And which distributions would you use for each component in the factorization? Explain.

\[\begin{align*} p_{A, C}(a, c) &= p_{A | C}(a | c) \cdot p_C(c) \quad \text{(Option 1)} \\ p_{A, C}(a, c) &= p_{C | A}(c | a) \cdot p_A(a) \quad \text{(Option 2)} \end{align*}\]

Hint: Think of which of the distributions already covered in the course you would use for each component of the joint distribution.

Part 3: Draw a directed graphical model for the joint data likelihood. Write down the log of the joint data likelihood (the joint probability of all \(N\) observations). Both should explicitly depict the parameters of the model that you’d like to learn.

Part 4: Implement your model in NumPyro. Perform the MLE on your model.

def IHH_CER_generative_model(N, a=None, c=None):
    pass # TODO implement

Part 5: Verify your model learned the data distribution well by visualizing each component of your joint distribution against the empirical distribution of the data, as well as the marginals (you can do this by histogramming data generated from your model).

Part 6: Help the researchers interpret your fitted model. Which conditions hinder telekinetic ability, and which enhance it? How can you tell?